
非線形とは何か-Fragile、Robust、Antifragileを理解するために-
以前の記事で、世の中には"非線形"なものがありとあらゆるところに潜んでいると書きました。 そこでは非線形性を「結果が長い停滞の末に一気に現れる」ことだと述べました。
今回は非線形についてもう少し詳しく話していきます。
世の中は非線形に満ち溢れており、非線形がむしろ"当たり前"です。 よって世の中を理解するために、非線形がどういったものであるかを知っておくことはとても重要です。
※数学的に非線形を取り扱うわけではないのでご注意ください。
非線形とは何か
非線形とは一言でいえば"直線でない"ことを表します。 線形とは直線のこと。 非線形はその否定形です。 (ダジャレではありません)
例えば下のグラフで表したものはすべて非線形です。
例えばタバコを1日に何箱も吸っていて突然末期の肺がんと宣告されることは、下図の青線のように非線形だと考えられます。
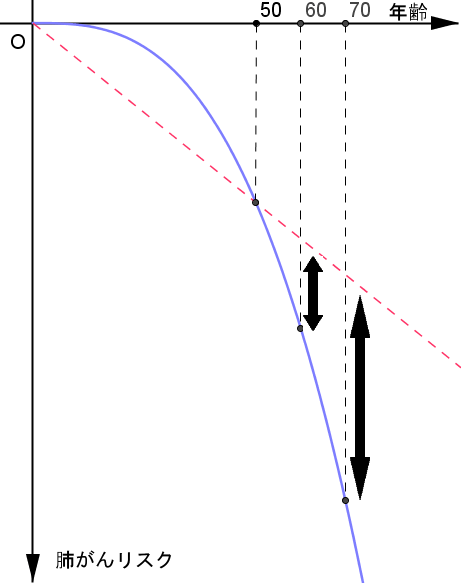
決して赤点線のように線形、直線ではありません。 だってタバコによる肺がんリスクは、20代、30代、40代あたりまでは少ないですが、50を過ぎてからグッと増えますよね。 そして60、70になるとグワッと高まっていきますよね。
もし直線的だったら、40代、50代、60代の間の肺がん人数の差は現実のように大きな開きはないはずです。
非線形だと、こういうグワッとした開きが可能になります。 図の太い矢印のように、線形と非線形との間には途中からものすごい差が開いていくことが物語っています。
非線形と凸関数
さて、非線形なグラフは凸関数というものから出来ています。 凸関数には次の2種類があって、これらいずれか1つだけ、またはこれらを2つ以上組み合わせて非線形が出来上がっています。
- 下に凸(Convex)
- 上に凸(Concave)
下に凸とは最初に示した5つの図の1番目と3番目のようなグラフを指します。 要はお茶碗型をした非線形なグラフを下に凸と言います。


逆に上に凸とは、下に凸を上下逆さまにした、お茶碗をひっくり返したグラフのことを言います。 最初に示した5つの図のうち、2番目と4番目が上に凸なグラフです。


ちなみに最初に示した5つの図の5番目は、下に凸なグラフと上に凸なグラフを組み合わせて出来ています。 下図のように、青色部分が下に凸、赤色部分が上に凸です。
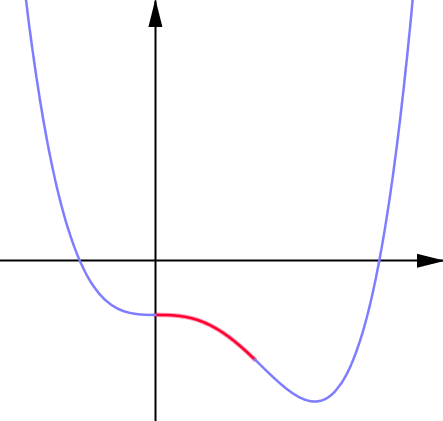
簡単に下に凸、上に凸を覚える方法があります。 それは下に凸はスマイルや笑い顔、上に凸はしかめっ面、怒った顔を表すのです。 口元に注目!


※1 ちなみにこれはタレブのアイデアを完全にパクリました。てへっ(下に凸)!
※2 (下に凸)=(笑) の意 ←上に凸! (おふざけ注釈にお怒りのようです)
下に凸だとスマイルというプラスイメージ、上に凸だとしかめっ面というマイナスなイメージというのは実はイメージの捉え方として重要です。 何故なら、最後に書いていますがAntifragileは下に凸の性質のもの、Fragileは上に凸な性質のものを表すのですから。
Fragile、Robust、Antifragileを理解するために大切な非線形がもつ性質
Fragile、Robust、Antifragileを理解するためには、非線形がもつ性質を理解することが何より重要になります。 そのために次の2つの非線形の性質を理解することはとても重要です:
- たった1回の結果がいままでの結果の合計を上回る
- ちょっとの変化が大きな変化を生む
以下、これら二つについて話していきます。
非線形の性質1:1回の結果がいままでの結果の合計を上回る
一つ目の非線形の性質は、1回の結果がいままでの結果の合計を上回ることです。
例えば下に凸な非線形なグラフを見てみましょう。 下図の「1」や「5」という数字は、何かしらの出来事だと思ってください。 数字が大きければ大きい程、より大きい出来事が起こったということです。
例えば「1」を分速60mの徒歩、「5」をその5倍、分速300mのダッシュだと思ってください。
一方f(X)は出来事が起こった時の結果を表します。 例えばf(X)を歩いた時に足腰につく筋肉量だと考えてください。 このときf(1)が分速60mで歩いた時に足腰につく筋肉量、f(5)は分速300mでダッシュしたときに足腰につく筋肉量です。
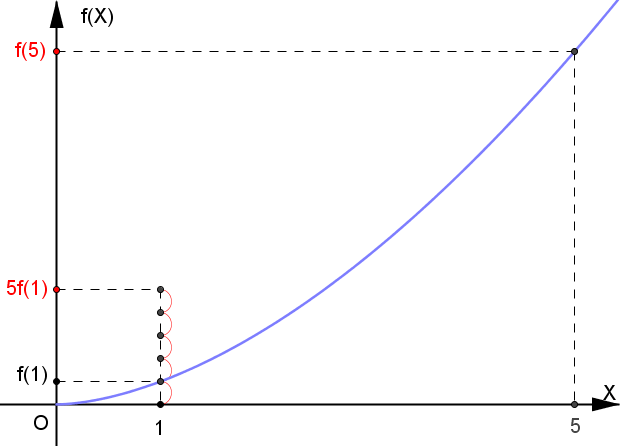
「1」の出来事が5回起こった時の結果が5f(1)(=5×f(1))、「5」の出来事が1回起こった時の結果がf(5)で表されています。 すると図からわかるように、5f(1)よりもf(5)の方が大きいですよね。 これは5回の結果の合計を、たった1回の結果が上回っていることを意味します。
分速60mで5分間歩くのと分速300mで1分間ダッシュするのでは、ダッシュの方が明らかに足腰につく筋肉は多いですよね。 こういうことです。
同じように上に凸を考えても、5g(1)よりもg(5)の方が小さいです。
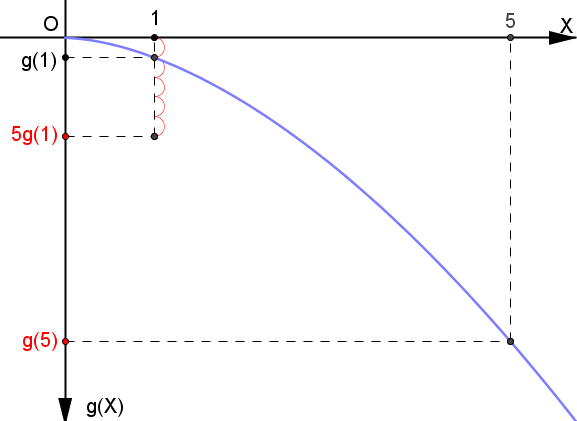
つまり規模が小さいことが5回起こったよりも、規模が大きい1回の方がマイナスの影響が強くなるのです。
具体的にイメージしてもらうために、雨の量と被害の関係を考えましょう。
九州では梅雨の時期、6月あたり大体300mm前後の雨が降ります。 しかし300mmがどのように降るかによって、被害の状況は大きく変わります。
もし毎日10mmずつの雨が30日間降ったらどうでしょうか。 こんな毎日シトシト雨が降ったところで、毎日傘が必要になって面倒くさい、気分が憂鬱になるくらいで大した問題にはなりません。
しかし6月のうち29日間が晴天で、残りの一日だけ集中的に300mmの雨が降ったらどうでしょうか。 土砂崩れ、道路冠水、床上浸水、列車の不通など、大きな災害に見舞われる可能性がぐっと高まります。
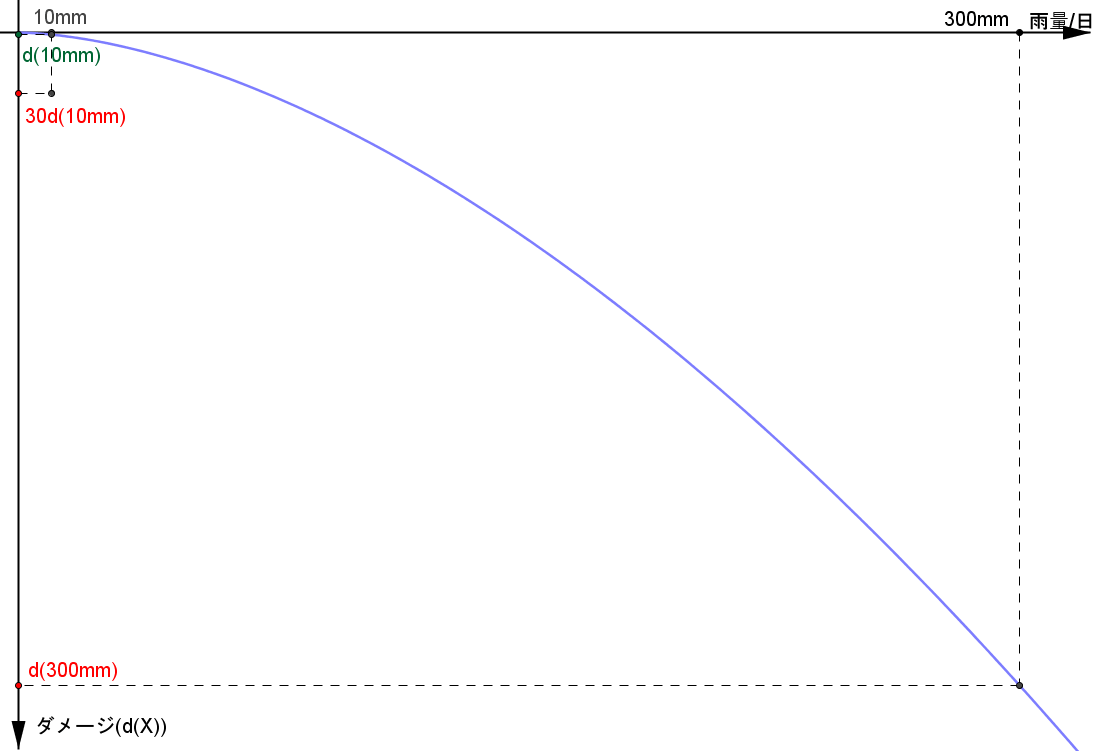
つまり非線形の性質である、1回の結果がいままでの結果の合計を上回ることが起こっているのです。
毎日10mmの雨が30日間降っても、一か月の間のたった1日だけ300mmの雨が降っても、6月に降った雨量はともに300mmで同じです。
しかし同じ雨量がもたらす結果は、二つの間に天と地との開きがあるのです。 (上のグラフでいうところの30d(10mm)とd(300mm)の差です)
非線形の性質2:ちょっとの変化が大きな変化を生む
非線形の性質2番目は、あるところを境にちょっとの変化が大きな変化を生むことです。
例えば次の下に凸な非線形なグラフを見て下さい。 点AとBの間の長さはとても短いですが、点f(A)とf(B)の高さの差は長いですよね。
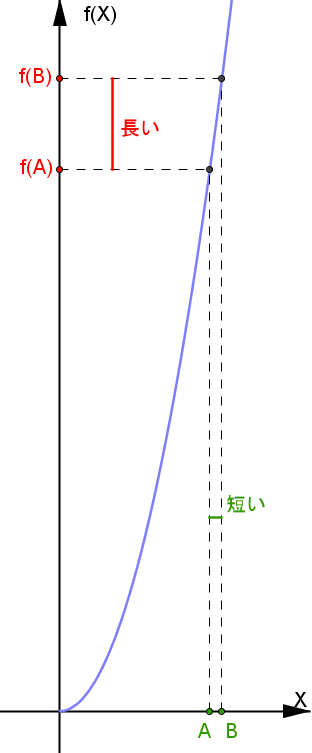
これがちょっとの変化が大きな変化を生むということです。 同じように上に凸の場合も、上のグラフを上下ひっくり返すことで同じことが言えます。
ちょっとの変化が大きな変化を生むことも、実は世の中ではごく当たり前のように起こっています。
例えば検索ページのクリック率。 Google検索を行うと1位から10位の順に検索結果が表示されますが、検索順位とクリック率との関係はは次のように表されます。 (青点線が実データ、橙線はその近似曲線)
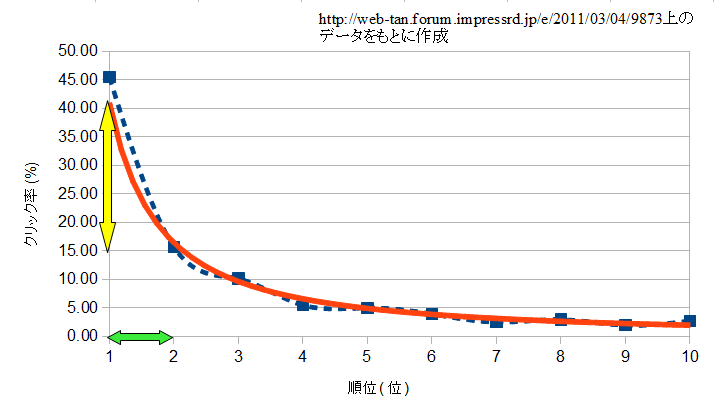
10位→9位、7位→6位だとクリック率に大した変化はありませんが、2位→1位のときのクリック率の変化が顕著ですよね。 順位が一つ移動しただけで、クリック率が実データだと15%→45%の3倍にまで増えています。
このようにあるところを境にして、たった一つの順位の変化がクリック率にめちゃくちゃ大きな結果を与えているのは非線形ならではの特徴です。
またマーケティングには「爆発点の理論」というものがあります。 これはある地域に集中的に店舗を構えて地域住民に認知が高まっていくと、あるとき突然売れ行きが急上昇する現象を指します。
例えばセブンイレブンは1995年から関西に店舗を構えるようになりました。 最初はライバルのローソンに大きく水を開けられていましたが、関西の店舗数が300店舗を超えたときに一気に認知度が高まり、利用者が急増したのです。 これにより関西のコンビニで1店舗あたりの平均日販がNo.1になりました。
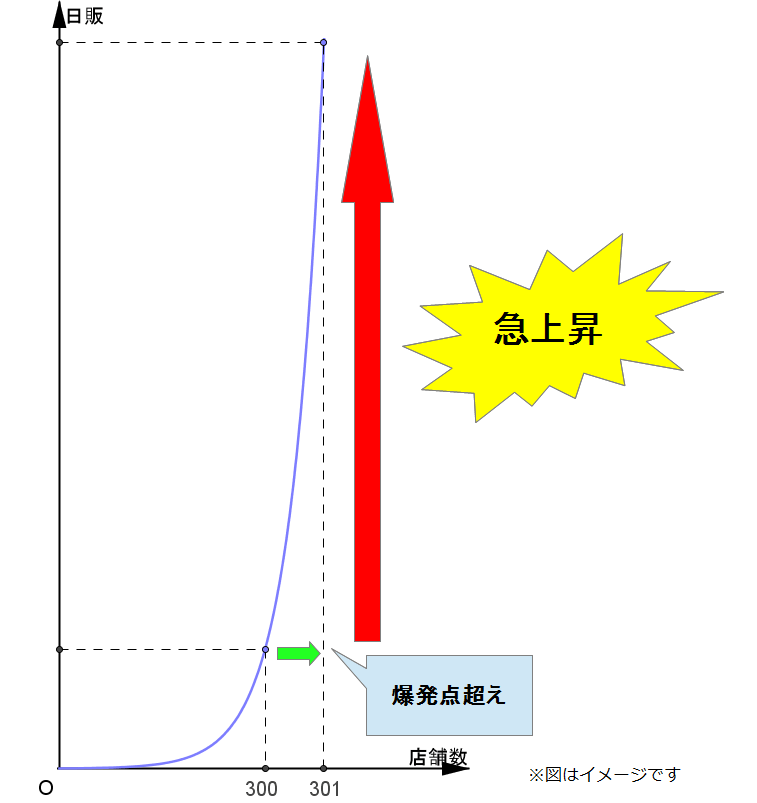
これだって非線形性による、ちょっとの変化が大きな変化を生む例です。 最初はどんなに店舗数を増やしてもほとんど効果はなくても、最後の一押しが認知度を急上昇させ一気にブレークを引き起こすのです。
Fragile、Robust、Antifragileの定義
最後に非線形の性質を取り入れたFragile、Robust、Antifragileの定義を紹介して終わりにします。
- Fragile:ちょっとした変化によって大きなダメージを受ける可能性があること(上に凸な性質をもつこと)
- Robust:どんなちょっとした変化によっても大きなダメージを受けないし、大きな利益を得ないもの
- Antifragile:ちょっとした変化によって大きなダメージを受けず、むしろ大きな利益を得られるもの(下に凸な性質をもつこと)
関連ページ
- Antifragileとは何か?
- 何故Antifragileが重要か-ランダムと非線形-
- 不確実を味方につけて大きな利益を得るための3要素
- 非線形とは何か-Fragile、Robust、Antifragileを理解するために-
- Fragile、Robust、Antifragileとは(理解を深めたい人向け)
- 職業によってリターンの度合いが異なる-Antifragileをブレンドする-
- 失敗とテクノロジー-テクノロジーはTrial and errorから生まれる-
- ベーコンの線形モデルとは-何故理論あってのテクノロジーなのか-
- 偶然とテクノロジー-理論とテクノロジーの非対称性-
- ランダムだから人生が楽しくなる
- 「努力は報われる」を考える-漠然を愛する考えの提案-
- 企業の目標はオプションが多い-企業と個人の目標の置き方の差異-
- 土壌を広げて成功を待つ-Antifragile的成功への考え-
- 犠牲と利益-大きな利益を得るためには必ず犠牲が伴う-
- 犠牲と利益-列車の安全性の裏に乗客の犠牲あり-
- 失敗は大きな利益を得るための情報
- 平均は求める場所ではない-尖ったものが合わさってバランスをとっている-
- Ludic fallacyとは-現実世界をゲーム的に捉える考えの過ち-
- Ludic fallacyと教育-学校で学ぶ確率はすべてゲームの世界-
- 経済学教-Economics rationalizes us-
- Known unknownsとUnknown unknownsとは
- 1920年代のアメリカバブルから見るバブルの正当化
- 専門家とFragile-1920年代のアメリカバブルから見える教訓-
- つながりの力-独立性の有無が大人数の選択の意味を変える-
- 自分で自分の文脈をつくる-成功本には必ず文脈がある-
- 帰納の問題と食品の安全性-被害が出るまで安全かどうかはわからない-
- レーシック手術と帰納の問題
- Iatrogenesis(医原病)とは何か-医者は別の病気を生む-
- 血液を医師に抜き取られて死んだ男、ジョージ・ワシントン
- 女性特有の病気とIatrogenesis-ヒステリー&マンモグラフィー-
- スウェーデンの結核死亡率の歴史-寿命を延ばす要因は医療だけではない-
- 生存率と死亡率の違い-医療と正しく付き合うために-
- リード・タイム・バイアスとレングス・バイアスとは
- 生存率は医療界の生存にプラスに働く
- 健康基準に根拠があるとは限らない、科学的に決められたとしても
- 医師の診断を確率的に考えてみる-Base rate neglect-
- 正しさを追い求めることの罠-正しさとFragile-
- 正しさを追い求めることの罠-正しさと心理との関係-
- 一次効果と二次効果とは-何故計画は現実を過小評価するのか-
- 不安定が安定をもたらす-人工呼吸器とJensenの不等式-
- 投資の教え、安全域の原則とAntifragile
- リスクとボラティリティとの違い-ボラティリティはリスクにも利益にも変化する-


