
一次効果と二次効果とは-何故計画は現実を過小評価するのか-
世の中には様々な場面で様々なモデルが使われています。 経済予測、新規鉄道の着工費、年金の給付見通しなどなど。 科学者たちが統計的にモデルをつくり、将来を見積もるのです。
しかしモデルによって得られた見積もりは、現実を過小評価していることがごく当たり前になっています。 公共事業の着工費が、当初見積もりよりも2倍にも3倍にも跳ね上がるなんて日常茶飯事ですよね。
こうしたことは単に見積もった科学者の能力が劣っているだけではありません。 もっと客観的で本質的な問題が隠されているのです。
キーワードは一次効果と二次効果です。
一次効果、二次効果とは何か
一次効果と二次効果とは何でしょうか。 何やら抽象的で難しそうですよね。
言葉は何やら難しそうですが、実際こいつらは別に難しいものではありません。 グラフを見ればすぐに解決です。
下図を見て下さい。
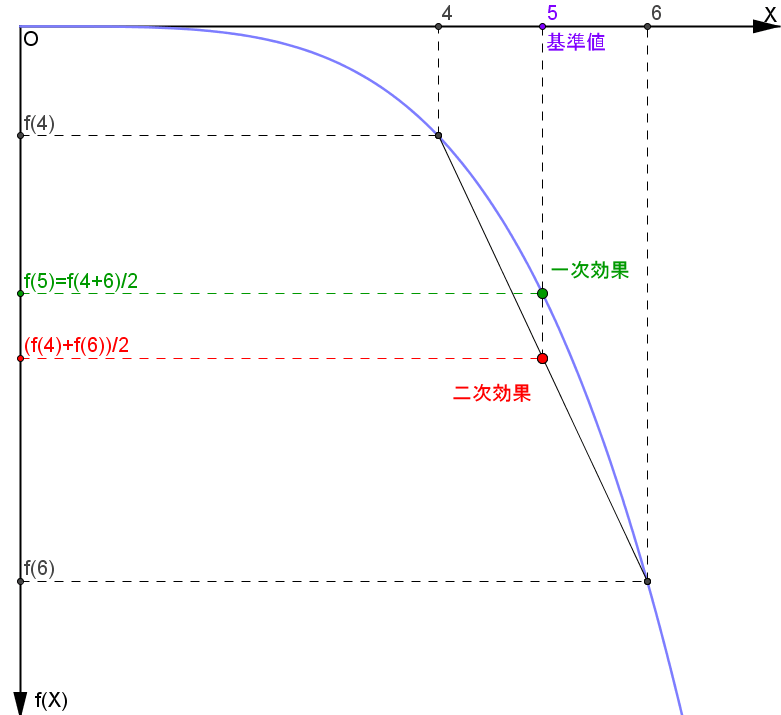
横軸のXは何かを調査するときに必要な変数、パラメータを表します。 例えば高速道路を建設するための難易度だと思ってください。
そしてf(X)はパラメータXが与えられたときの欲しい結果を表します。 例えば高速道路建設の難易度に応じた建設費用だと思ってください。
上図の緑の点が一次効果、赤の点が二次効果です。 つまりf(5)が一次効果、(f(4)+f(6))/2が二次効果です。
f(5)の中身の「5」という数字は、図にあるように何かしらの基準値を表しています。 例えば「5」は高速道路を建設するための予想難易度だと思ってください。
そうすると、一次効果のf(5)は「予想した難易度で必要な高速道路建設費用」を表します。
一方「4」と「6」はそれぞれ5からのズレです。 予想した難易度よりも1段階少ないのが「4」、1段階多いのが「6」だと思ってください。 するとf(4)、f(6)はそれぞれ、見積もり難易度より1段階ずれたときの高速道路建設費用となります。
そうすると、二次効果である(f(4)+f(6))/2は「予測難易度がズレたときの建設費用の平均」を表します。
要するに一次効果は「基準や平均から得られる結果」、二次効果は「基準や平均からズレたときの"結果の平均"」のことです。
一次効果は学者が算出するもの、大切なのは二次効果
一次効果は学者が算出する結果です。 「5」というパラメータの基準値をまず考えて、その基準値を学者が作ったモデルに当てはめて一次効果を求めるのです。
例えば厚生労働省によって行われる財政検証では、将来の物価上昇率や賃金上昇率といった複数のパラメータの基準値をまず考えます。 そしてこれら基準値を計算モデルに当てはめて、将来の年金給付額を見積もっています。 つまりここでは年金給付額という一次効果を求めているのです。
しかしもちろん将来の物価上昇率や賃金上昇率は、財政検証の段階ではわかりません。 きっとこうなるだろうと基準値を"決め打ち"して年金給付額という一次効果が見積もられます。
私たちにとって本当に大切なのは二次効果です。 何故なら二次効果は、見積もりに使ったパラメータが万が一基準値からズレた場合に、どの程度結果に影響を与えるかを私たちに教えてくれるからです。
将来のパラメータが基準値からズレるのはごく普通です。 よって基準値がズレたときの影響を考慮した二次効果が大切となるのです。
そこでナシーム・タレブはあらゆるモデルの脆弱性、Fragile性を考える上で"一次効果と二次効果の差"を考えることを推奨しています。 一次効果は科学者が見積もった数値、一方で二次効果は、科学者の見積もりのエラーを考慮したより現実的な数値です。
つまり一次効果と二次効果との差を考えることは、言うなれば"予想と現実とのギャップ"を考えるということです。 ギャップが大きければ大きい程、予想よりも現実が悪くなる傾向にあることを意味するのです。
何故予測や計画は現実を過小評価するのか
世の中には無数の計画がありますが、計画通りに物事が動くことはほとんどありません。 現実は概して計画よりも悪いものです。
例えば新幹線の建設費を見てみましょう。 東海道新幹線の建設費の予算は利子等も含めて1972億円でした。 しかし最終的な建設費はその2倍、3800億円にまで膨れたのです。
上越新幹線に至っては、当初の建設費は4800億円でしたが、トンネルの建設に予想以上苦しんだこともあり、結果的に当初の3.5倍以上の1兆7000億円にまで跳ね上がったのです。
一方九州新幹線は当初計画が6400億円、実際が6300億円でした。 ほぼ計画通り、むしろ当初計画よりもよい結果となっています。
しかし良いといってもたったの100億円、当初の建設費より1.16%減っただけ。 当初計画よりも費用が100%増えた東海道新幹線、250%増えた上越新幹線と比べれば微々たるものです。
このように予測や計画に比べて、実際はそれ以上にダメージが増えるもの。 しかもダメージは2倍、3倍にもどんどん膨れ上がっていくのです。
その逆に予測や計画が現実に比べて良かったケースは多くありません。 しかも例え良かったとしても、得はそんなに増えないのです。
何故でしょうか。 それは非線形でFragileだからです。 そのため次の二つのリスクをどうしても抱えてしまうのです:
- 一次効果と二次効果の差が開いてしまう
- 得は限定的、損は天井知らず
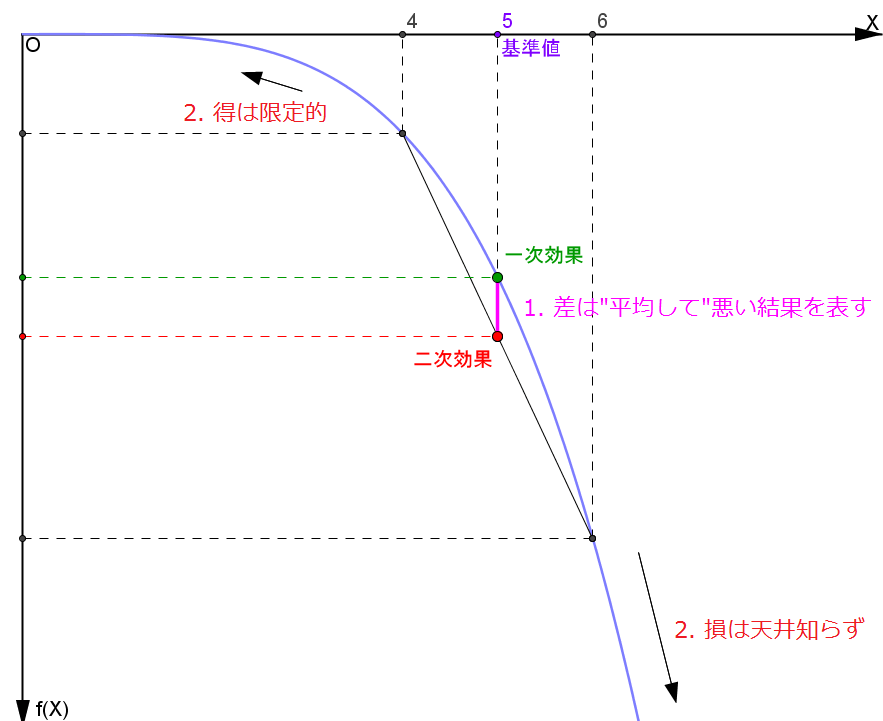
まず非線形だと一次効果と二次効果の差が開くのは必然です。 一次効果と二次効果の差が開いているというのは、「予想よりも現実の方が平均して悪い」ことを意味します。 開けば開くほどもっと悪くなります。
つまり予測よりも悪い結果が出やすくなるのは、例え予測に使ったモデルが正確で予測をちゃんと行っていても免れることが出来ないのです。
しかも予想外の出来事、例えば岩石が予想以上に硬かったり考えてもいなかった湧水によってトンネルの建設に苦しめば苦しむほど、ダメージは飛躍的に増えていきます。 損は天井知らずなのです。
一方で得は限定的です。 これはFragileの上に凸な性質からそう言えてしまいます。
こういうことを考えると、予測や計画よりも厳しい現実になることは"必然"なのです。
***********
もちろん、最初の予測をかなり厳しめ、将来を悲観的に見れば予測と現実の乖離は減るかもしれません。 予測や計画よりも、実際の建設費を安く抑える可能性を増やせるかもしれません。
でもそんなこと、上の人、承認者が許すと思いますか? そんな悲観的な予測や計画をして、承認者は気分がいいと思いますか?
こうした心理的な面も考えると、予測や計画よりも現実はずっと悪いと考えたほうが良さそうです。
関連ページ
- Antifragileとは何か?
- 何故Antifragileが重要か-ランダムと非線形-
- 不確実を味方につけて大きな利益を得るための3要素
- 非線形とは何か-Fragile、Robust、Antifragileを理解するために-
- Fragile、Robust、Antifragileとは(理解を深めたい人向け)
- 職業によってリターンの度合いが異なる-Antifragileをブレンドする-
- 失敗とテクノロジー-テクノロジーはTrial and errorから生まれる-
- ベーコンの線形モデルとは-何故理論あってのテクノロジーなのか-
- 偶然とテクノロジー-理論とテクノロジーの非対称性-
- ランダムだから人生が楽しくなる
- 「努力は報われる」を考える-漠然を愛する考えの提案-
- 企業の目標はオプションが多い-企業と個人の目標の置き方の差異-
- 土壌を広げて成功を待つ-Antifragile的成功への考え-
- 犠牲と利益-大きな利益を得るためには必ず犠牲が伴う-
- 犠牲と利益-列車の安全性の裏に乗客の犠牲あり-
- 失敗は大きな利益を得るための情報
- 平均は求める場所ではない-尖ったものが合わさってバランスをとっている-
- Ludic fallacyとは-現実世界をゲーム的に捉える考えの過ち-
- Ludic fallacyと教育-学校で学ぶ確率はすべてゲームの世界-
- 経済学教-Economics rationalizes us-
- Known unknownsとUnknown unknownsとは
- 1920年代のアメリカバブルから見るバブルの正当化
- 専門家とFragile-1920年代のアメリカバブルから見える教訓-
- つながりの力-独立性の有無が大人数の選択の意味を変える-
- 自分で自分の文脈をつくる-成功本には必ず文脈がある-
- 帰納の問題と食品の安全性-被害が出るまで安全かどうかはわからない-
- レーシック手術と帰納の問題
- Iatrogenesis(医原病)とは何か-医者は別の病気を生む-
- 血液を医師に抜き取られて死んだ男、ジョージ・ワシントン
- 女性特有の病気とIatrogenesis-ヒステリー&マンモグラフィー-
- スウェーデンの結核死亡率の歴史-寿命を延ばす要因は医療だけではない-
- 生存率と死亡率の違い-医療と正しく付き合うために-
- リード・タイム・バイアスとレングス・バイアスとは
- 生存率は医療界の生存にプラスに働く
- 健康基準に根拠があるとは限らない、科学的に決められたとしても
- 医師の診断を確率的に考えてみる-Base rate neglect-
- 正しさを追い求めることの罠-正しさとFragile-
- 正しさを追い求めることの罠-正しさと心理との関係-
- 一次効果と二次効果とは-何故計画は現実を過小評価するのか-
- 不安定が安定をもたらす-人工呼吸器とJensenの不等式-
- 投資の教え、安全域の原則とAntifragile
- リスクとボラティリティとの違い-ボラティリティはリスクにも利益にも変化する-


