
損得行動4パターンをグラフで理解する-取得×低確率-
前回紹介した損得行動4パターンを今度はグラフを使って説明します。 1枚の絵は1000の言葉に値するというくらいですからね。 これによってプロスペクト理論のより深い理解の手助けになれば幸いです。
①取得×低確率
例えば次のようなギャンブルがあったとしましょう:
床に100個の箱があります。 そのうちの1箱にだけ100万円が入っており、残りの99箱は空です。 この100個の箱の中から、1箱だけ選んでください。
要は1%の確率で100万円が当たるギャンブルとなっています。 このとき私たちがこのギャンブルに対して感じる価値は下図の点B(赤丸)になります:
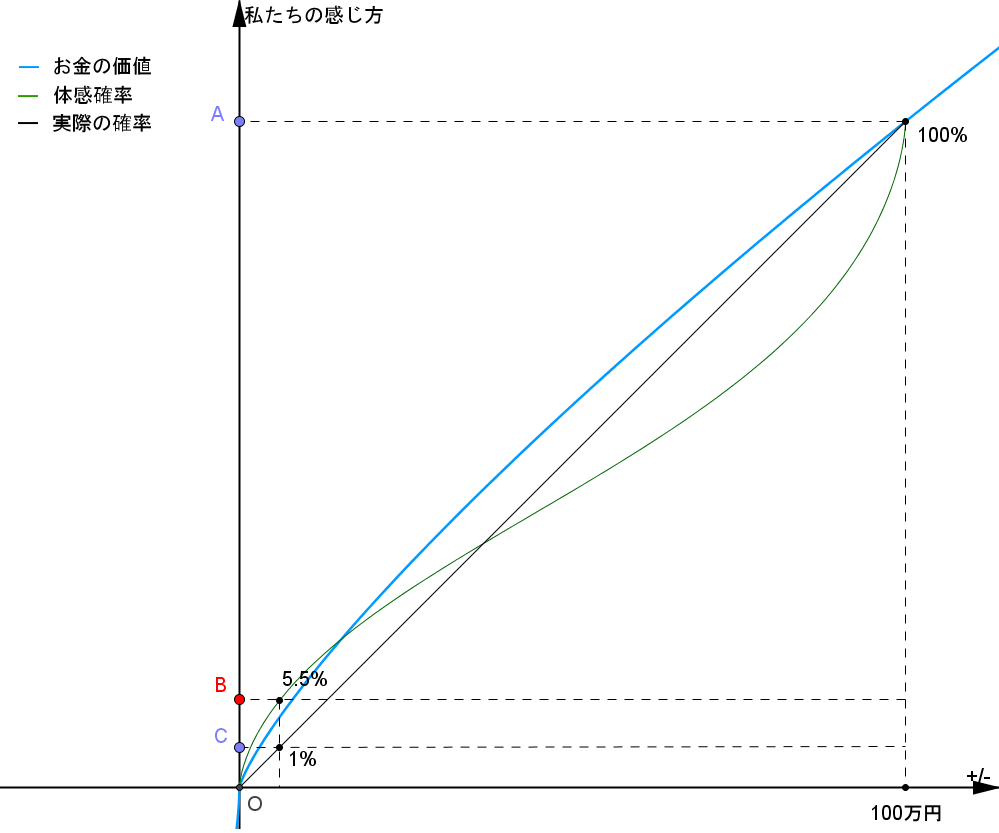
点Aは100万円をもらえたときに感じる価値を表します。 しかし上のギャンブルでは100万円をゲットできる確率は1%ですから、このギャンブルに対する価値はもちろん点Aよりも低いです。
点Cは「文字通りの」1%の確率で100万円をゲットできるというギャンブルに対する価値を表します。 もしも私たちが確率を数字通りにちゃんと捉えていれば、上のギャンブルに対して感じる価値は(100万円をゲットしたときの価値)×1%となるはずです。
しかし以前の記事で話したように、私たちは低確率を実際はもっと高確率に感じてしまうことが多いです。 実際には1%なのに、体感では5.5%ともっと高い感覚で確率を捉えてしまいがちです。
そのため上のギャンブルに対して感じる価値は、点Bの位置になるのです。 点Bが点Cより高いところにあるのがポイントです。 低確率に何かをゲットできるギャンブルに対しては、実際よりも高い価値を見積もってしまうのです。
これがプロスペクト理論が表す「取得×低確率→過大評価」を視覚化したものです。
二つのギャンブルを比較する
今度は次の二つのギャンブルを比較してみましょう:
- 確実に1000円もらえる
- 1%の確率で10万円もらえる
このときどちらのギャンブルを選択しますか? もちろん人によってまちまちだとは思いますが、私だったら2番目を選択して10万円に賭けます。
理論的には二つのギャンブルに有利不利はありません。 どちらも期待値が1000円だからです。 二つは同等なギャンブルなのです。
しかし人間心理から考えると、上の二つのギャンブルは決して同等ではありません。 下図のように二つのギャンブルに対する感じ方は異なっているのです:
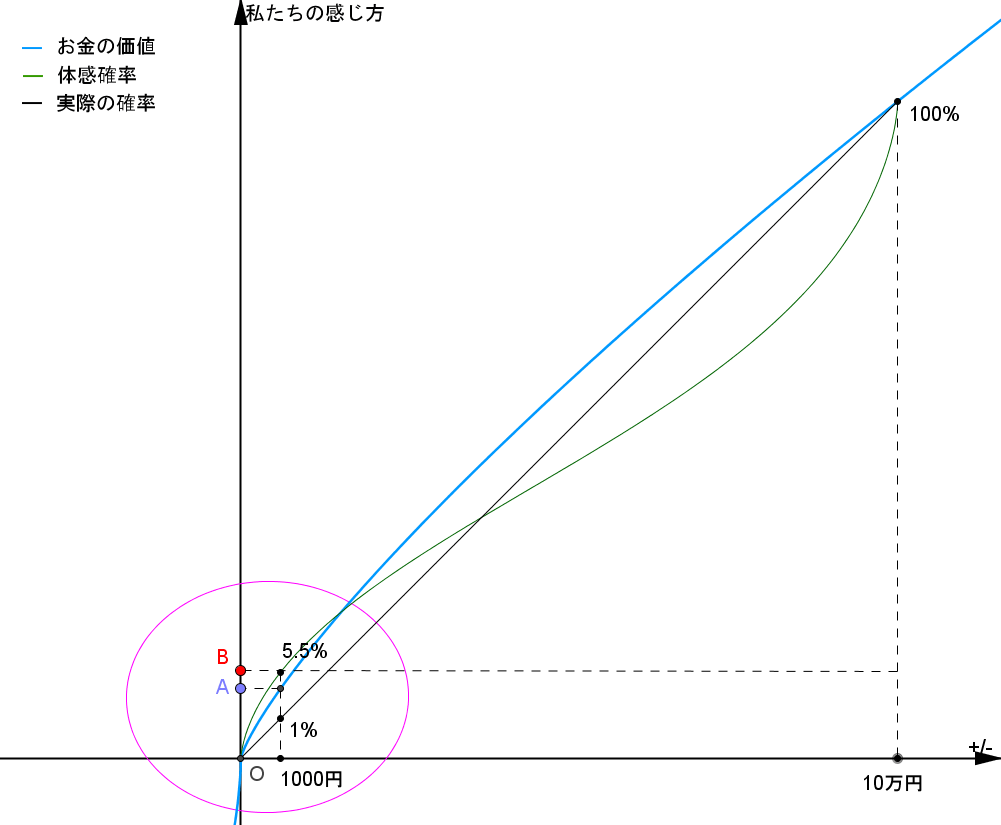

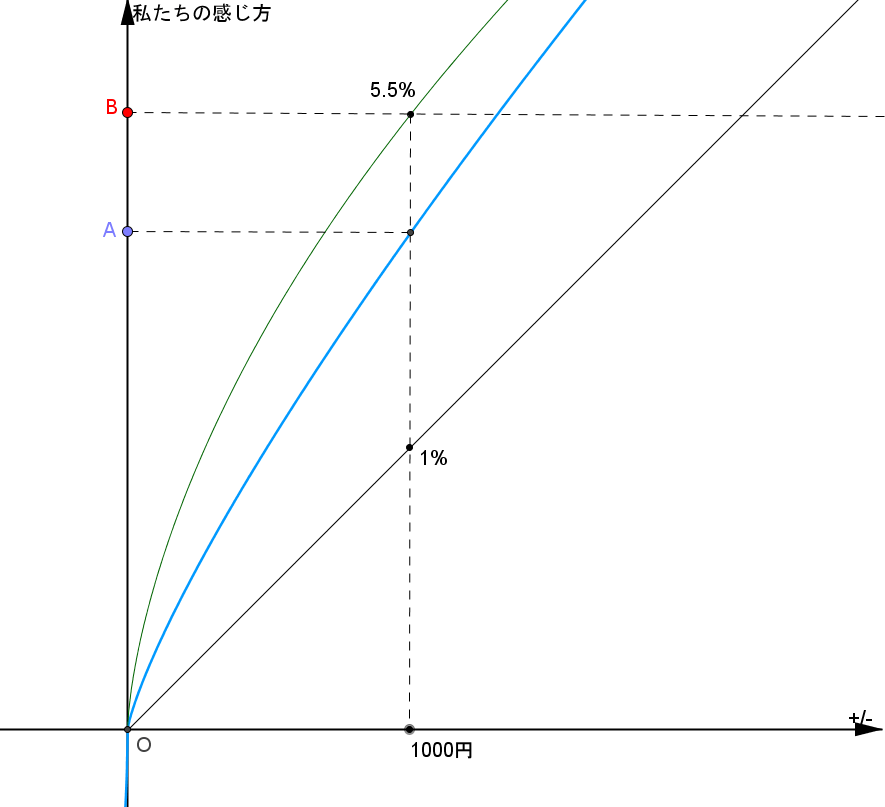
点Aが確実に1000円もらったときに感じる価値です。 そして点Bが1%で10万円をもらったときに感じる価値です。
点Bが点Aよりも上に来ているので、この場合は1%の確率で10万円もらえるギャンブルの方が魅力的になります。
私たちはあえて確実なものを棄てて低確率な方に賭けることがありますが、それはプロスペクト理論のグラフを使えば上のように説明できます。
常に低確率が魅力的なわけではない
最後に、場合によっては低確率な方に常に賭けるわけではないことを見てみましょう。 次のような2つのギャンブルを考えます:
- 確実に150万円もらえる
- 1%の確率で2億円もらえる
この二つだったらどちらを選択しますか? 合理的に考えれば4番を選択するほうが賢いです。 何故なら4番のギャンブルの期待値は200万円で、3番のギャンブルの期待値の150万円よりも大きいからです。
しかも体感的に1%を5%と感じたりするものですから、このときの4番のギャンブルの体感期待値は750万円にもなります。 そう考えると多くの人は4番を選択するのでしょうか?
いえ、決してそうではないでしょう。 上の二つだったら確実に150万円をゲットしたいと思う人だっていっぱいいるはずです。 何故なら150万円というお金は巨額だからです。
下のグラフを見て下さい:
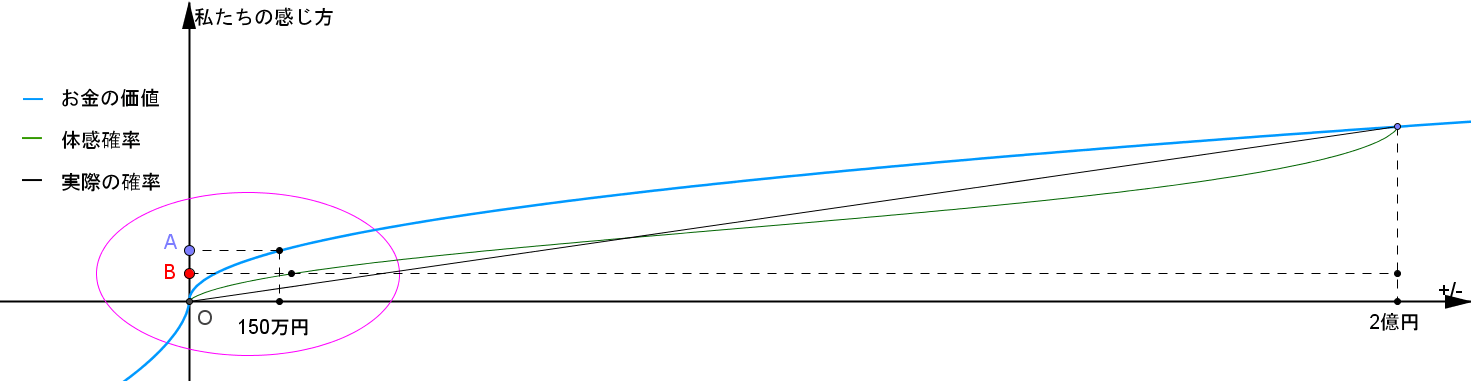

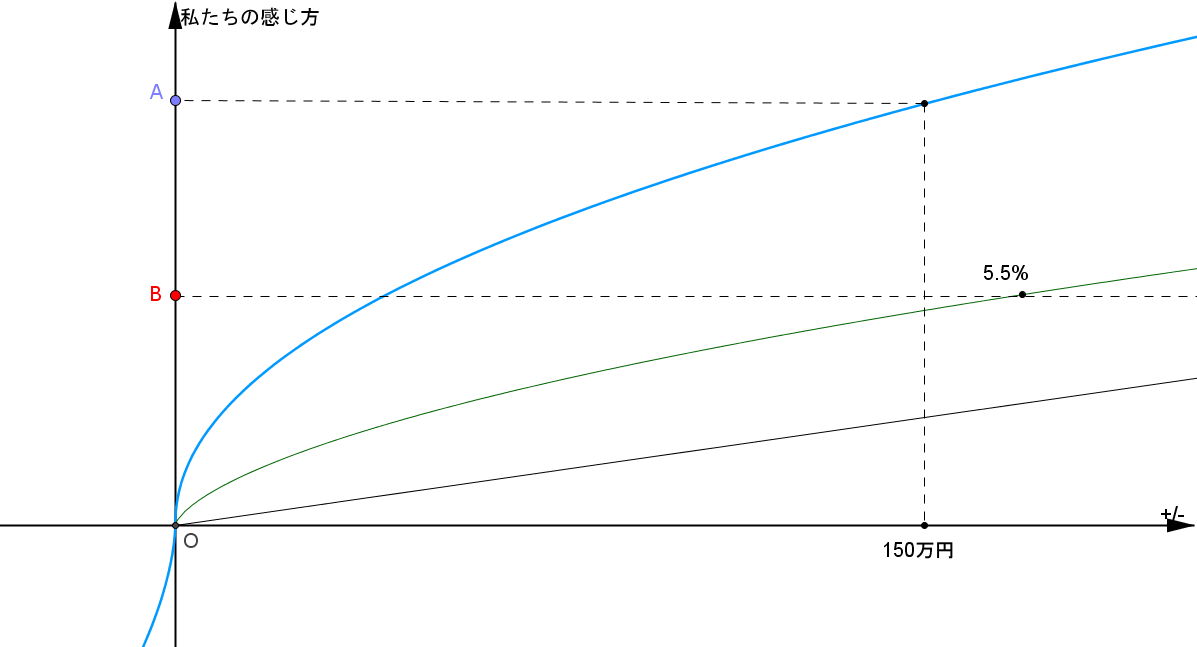
点Aが確実に150万円もらえることに対する価値、点Bが1%で2億円もらえるギャンブルの価値です。 この図では点Aの方が点Bよりも高い位置にあるため、確実に150万円もらえる方が価値を感じています。
こうなる理由は何でしょうか? 理由は青いグラフがS字カーブを描いている(Diminishing sensitivity!)からです。
150万円と2億円、多くの方々にとってはともに大きな金額です。 S字カーブが表しているように、参照点(原点O)から離れれば離れるほど感じる価値の変化はなだらかになっていきます。
150万円というのが既に大きな金額なので、150万円→2億円ときに感じる価値の変化の大きさが抑えられるのです。 なので上のように確実に150万円もらえる方をチョイスする人が増えるのです。
いくら1%を体感で5.5%と感じようとも、だからといって低確率なものを常に好むわけではないです。 こういう人間心理もしっかりプロスペクト理論には反映されていることに注意してください。
※注意:人によっては2億円の賭けの方を好む人ももちろんいます。
関連ページ
- プロスペクト理論とは何か
- プロスペクト理論をもっと理解する-グラフから見える3つの要旨-
- 参照点-人の感情は比較で生まれる-
- Diminishing Sensitivity-損得感情は緩やかになっていく-
- Loss aversion-失うなんて絶対に嫌だ-
- 確率なんて信じられない!-実際の確率と体感確率との乖離-
- 確率際でのインパクト
- 損得行動4パターン
- 損得行動4パターンをグラフで理解する-取得×低確率-
- 損得行動4パターンをグラフで理解する-損失×高確率-
- 何故傷口が大きいほどより傷口を広げる行動を取るのか
- 何故プロスペクト理論は重要なのか
- プロスペクト理論はどのようにして生まれたのか-Expected Utility理論の過ち-
- Loss aversionは生存するための一種の能力
- Loss aversionと言葉-プラス感情よりもマイナス感情の方が表現豊か?-
- 幸せはストックされにくいが損は簡単にストックされる
- 大きな幸せ、大きな悲しみ、トラウマ
- Sunk-Cost Fallacyとは-何故ベテラン選手はひいきされるのか-
- Sunk Cost Fallacyとトップの人たち-膨大な二次コストを払うのは私たち-
- Sunk-Cost Fallacyと意思決定-諦めたらそこで試合終了?-
- 愛着、プライスレス
- 質素でいることが最強の生き方-プロスペクト理論から考える暮らしのありかた-
- 質素でいることが最強の生き方-Lossを減らして安全域を広げる-
- 質素でいることが最強の生き方-デメリットを考える-
- Denominator neglect-見せ方で受取り方は変わる-
- はっきりしてると何となく起こりそうな気がする-Ellsbergのパラドックスと透明性-


